Math Professional Development for Teachers
Become the math teacher you always wished you had.
Learning for the Long-View is a powerful platform that can equip you to teach, learn, and think about math in new ways. Built on the desire to help children generate a framework for arithmetic that is founded on reasoning and has a robust connection to algebra, we have worked to “unlearn” how arithmetic is typically taught—as a set of procedures that are disconnected from their core concepts and separated by number form—and move forward, instead, supporting young mathematicians to conceptualize arithmetic with a direct tie to algebra.
Additionally, through our innovative micro school we have worked to create classrooms in which discourse and reasoning are central, providing a math experience that builds confidence, reasoning, self-efficacy, communication, and collaboration.
Learning for the Long-View is a place where you can re-build your own conceptual framework to ensure a coherent link across all number forms, bridging arithmetic to algebra, as well as study videos of teaching in action, download lesson plans, read articles, and analyze student work. Learning for the Long-View will support you in becoming the math teacher you have always wanted to be. Join us now!
As a member, you'll have access to a dynamic library of videos, guides, graphics, scripts, and our "follow a band."
CHOOSE A PLAN
Reach out to us at admin@long-view.com with questions and for group pricing or a site-license for your school or district.
Get to know us.
Watch our Welcome Series and look over other examples of content to better understand the Learning for the Long-View membership.
Start Here.
Welcome
We're In It With You
Math for the Long-View
Set Yourself Up For Success
Next, look over some sample content. You’ll access even more as a member!
Construct Understanding Video #6: Do We Have Like Terms?
Using Language That Supports Mathematical Understanding
Graphic or Anchor Chart Supporting Active Learning
Follow Violet Band Video During Week 8: 100 Chart Public Share
Online Math Professional Development for Teachers
The discipline of mathematics has extraordinary potential for developing children’s capacity for learning because it is complex and challenging.
With the support of Learning for the Long-View, teachers have access to videos, articles, lesson plans, and resources that offer a chance to learn how to transform teaching and create a mathematics classroom that nurtures deep conceptual understanding, reasoning, critical listening, and collaboration.
What’s Included in Your Membership
A Rich Video Library
Our casual videos invite you to think differently about math. Start by perusing our twelve videos that construct a Generative Framework, and then shift into other categories of videos that help you expand and strengthen your mathematical reasoning or consider how you might impact the learning of others.
Guides & Graphics
Browse through reading materials, tips, and visuals that will support you as you really dig in. Read more about the powerful way we use language, download an anchor chart that might help in your classroom, or watch a classroom episode while analyzing the script so that you can better identify the moves that solicit deep thinking.
Weekly Lesson Plans
On our Follow a Band page, we’ll supply you with weekly lesson plans from one of classrooms and provide videos that support you in enacting the plans in your own classroom. The content from Follow a Band can be converted to your own day-to-day plans or used as math professional development, providing you or your school team with opportunities to analyze the way a Long-View Math Block unfolds over a year.
After years of teaching in both public and private schools, as well as engaging in a deep study of research on math education in particular and learning theories in general, we established four assumptions about learning that serve as the philosophical foundation for Long-View Micro School.
In considering the teaching and learning of mathematics, not only were we unable to find a curriculum that honored our assumptions, we also recognized that to be true to our assumptions it only made sense to call on our educators to act as creators in designing and implementing opportunities for learners to engage in the discipline of mathematics.
With this, we created our Generative Framework for Mathematics. The power of our Framework is that it is applicable to all number forms and removes the need for instruction focused merely on discrete procedures, a mainstay of American schools. The Generative Framework means children are not restricted to only learning “grade-level-based school mathematics;” they experience math as a connected discipline and reasoning is unleashed.
CHOOSE A PLAN
As a member, you'll have access to a dynamic library of videos, guides, graphics, scripts, and our "follow a band."
Reach out to us at admin@long-view.com with questions and for group pricing or a site-license for your school or district.
Goodbye textbooks and workbooks,
Hello Learning for the Long-View.
Finally, a different way to learn, teach, and grow.
When you join as a member, you’ll have access to a library of math professional development videos like these:
Common Questions
-
After years of teaching in both public and private schools and engaging in a deep study of research on math education in particular and learning theories in general, we committed to start an innovative micro school that would bring our new vision of learning—as well as our vision for a coherent and transformative experience in mathematics—to life.
Long-View Micro School was founded on four key assumptions about learning that serve as the philosophical foundation for the school and all subject areas. Over the course of more than ten years, the Long-View team—unable to find a mathematics curriculum that honored Long-View’s assumptions—worked to develop the content, culture, and pedagogy to support these core assumptions. The team worked to develop a framework for arithmetic that was founded on reasoning and had a robust connection to algebra, and to create classrooms in which discourse and reasoning were central. In turn, they saw Long-View learners growing tremendously as creators, communicators, collaborators, and critical thinkers as they constructed understanding of the concepts and methods of reasoning of mathematics.
The Long-View team recognized that the discipline of mathematics had extraordinary potential to develop children’s capacity for learning because it is complex and challenging. This fueled Long-View’s Generative Framework for Mathematics and the Long-View Learning Philosophy. Over the years as the Long-View team developed and refined the mathematics program, it became recognized for its unique focus on deep conceptual understanding, coherence across arithmetic to algebra, and reasoning. Further, the dialogic nature of the school’s pedagogy—perhaps most remarkable in math classrooms—provided an opportunity for children of Long-View to develop characteristics such as critical listening, perseverance, reasoning and self-efficacy.
Visitors, education leaders, and researchers observing Long-View’s math classrooms pressed the Long-View team to offer professional development to other schools and to other teachers, as well as to create a supportive online platform. Learning for the Long-View provides the furthest reach of the team’s work, and through The Number Lab, schools and teachers seeking in-person workshops and intensive PD and coaching, work toward implementation.
-
We offer both in-person and online professional development for math teachers.
Our in-person PD encompasses both consulting and workshops; it runs through our organization called The Number Lab. The Learning for the Long-View platform holds all of our online support.
In combination, teachers and schools that attend our summer workshops and hire us to consult at their schools—while also leveraging the Learning for the Long-View membership platform—experience the most transformative changes in their classrooms.
-
The power of our Generative Framework is that it is applicable to all number forms and removes the need for instruction focused merely on discrete procedures, a mainstay of American schools. The Generative Framework means children are not restricted to only learning “grade-level-based school mathematics;” they experience math as a connected discipline and reasoning is unleashed.
Long-View’s Generative Framework for Mathematics is rooted in unitization, growing an understanding of number by conceptualizing multiplication, addition, subtraction, and division, allowing for ways of reasoning that: 1) Create connections, 2) Transfer across number forms to algebraic reasoning, and 3) Establish a foundation for engaging in the discipline of mathematics.
Through supportive videos, articles, and resources, the Learning for the Long-View platform will help members understand and utilize this transformative framework.
-
Learning for the Long-View offers a wealth of resources, videos, and ideas. We recommend you start by watching our twelve short videos in the series “Construct a Generative Framework for Mathematics.” As you study these videos, you’ll be introduced to a new way of thinking in mathematics built on the power of unitization. After watching and studying, you might also read our guide on the same topic so that you understand the underlying logic even more clearly.
Next, peruse articles on how Language Supports Understanding and the Culture of a Long-View Math Block. Consider returning to the video resources in the Expand & Construct section or the Impact section. Browse through Follow Violet Band, and return again and again to view Guides, Graphics, and Scripts in our resources section.
Unlike traditional PD, you’ll be stretching yourself as a mathematician and analyzing ways you could be a more effective teacher. You can utilize the videos and resources alone, you can learn in collaboration with colleagues, or you can take what you are seeing and try it out in your own classroom.
-
This is an effort to help you create knowledge structures within mathematics that provoke understanding—understanding that leads to the generative use of knowledge, which means it is flexible, appropriate, and creative.
As best we can, we are working to support you to do this work yourself, so that you can then help others do it. If you construct a Generative Framework and then work to expand and strengthen your reasoning, you will be more equipped to impact others.
As you begin to understand how you can impact the learning of others, it is important to recognize that learning is best done with others. Thus, understanding how the “content” of mathematics can be different is only one part of this; ultimately, Learning for the Long-View involves constructing knowledge within a learning community.
That being said, this brings us back to your original question: Is this a math curriculum? Not exactly—this is more about you taking back your own teaching and learning so that you are better equipped to make the complex decisions that are inherent in teaching, but are often radically over-simplified in textbooks and curricula.
However, if you want to emulate what we do in our classrooms in your own, or with children you teach, you can use the weekly lesson plans on our Follow a Band page. The year’s worth of plans gives you incredible insight into our pedagogy, content, culture, and assumptions and will help you as you approximate the units of study that are foundational in our work. The band you’ll follow across the school year is called Violet Band and much of the crucial conceptual development happens within this band. Thus, you’ll have clarity on how we approach each concept and how we help our learners construct deep understanding and develop robust reasoning skills. In addition, the mathematical terrain this band interacts with over the course of a year is quite high, which makes the following Violet Band helpful to teachers and parents working with most elementary and even middle school learners.
-
We are math teachers, school leaders, and consultants. We’ve taught in public and private, started our own innovative micro school, and worked with educators and leaders across the world in workshops and coaching sessions. Along the way we tackled changing the experience students have in elementary and middle school math. We thought deeply about the shifts in content and practice that are needed in order to create a learning experience that is authentic to the discipline of mathematics—one based on deep understanding of concepts where reasoning, proof, and justification are a daily part of the class experience —and conceived of our Generative Framework that allows learners to take a critical approach to their work, increasing the ability to think flexibly and offer mathematically sound justifications of their thinking.
In working in a range of school settings, we’ve learned more about the inherent link between classroom culture and school culture, and we confronted the fact that to bring our vision to life we would have to start a new school. Long-View Micro School was born from this push against the status quo, with a desire to thoughtfully tie the assumptions our team has about children to the learning environment in all classes, but especially mathematics.
The Long-View team works collaboratively to bring content to members at Learning for the Long-View with the hope that anyone, anywhere can experience the magic of Long-View classrooms and have the opportunity to leverage this unique platform to access high-quality online professional development to initiate and sustain change.
-
At the core of Long-View’s work is a set of assumptions that have transformed the experience of teaching and learning for kids, parents, and educators. Assumption number one is that we believe children have significant capacity to understand many of the complexities of the world in which they live. Our other assumptions get to the heart of how we teach. Most schools view learning as acquisition and have strong behaviorist underpinnings. Long-View is revolting against this outdated formula of schooling; we design so as to reverse what Richard Elmore termed “the progressive dissociation between learning and schooling.”
Assumption #1: Children have significant capacity for understanding
Here are ways we work to live out this assumption:
*We take student thinking seriously.
*We hold an optimistic view of a child's ability to learn and the potential for change.
*We give responsibility for learning to the learner and we directly teach into this end. Responsibility for learning entails taking more control over your own mental activity and believing that ultimately you are responsible for your own learning and that you can affect the level of your learning.
*We do not focus on grade levels or ages when grouping children or planning content.
*We help our learners make use of their capacity by learning how to engage in effortful learning and how to learn with intentionality.
Assumption #2: Deep understanding derives from being a producer
Here are ways we work to live out this assumption:
*Learning is an active process and we want children spending their time creating, wondering, making, and conjecturing.
*The “products” of learning that we most value are intellectual products that are generated by the learners, including collective knowledge.
*“How and why” are important, and teachers engage learners in discourse that helps them reason.
Assumption #3: Learning is more powerful as a community endeavor
Here are ways we work to live out this assumption:
*We structure classrooms as learning communities in which the construction of knowledge is supported as a common goal.
*All students are accountable for participating in an intellectual climate characterized by argumentation that forwards deeper learning for all.
*We create classrooms where expertise is distributed. Everyone contributes his particular expertise in the discipline, as well as around learning and teaching. We are sharing the resources of everyone in the room.
*Discourse is a key. The discourse genre focuses on argument, questions, reflections, queries, interpretation, and criticism and it is the mode, rather than the exception.
*We make much of the learning and thinking public. Work is often analyzed by peers in order to both advance the knowledge of the entire community as well as enhance the individual’s learning.
Assumption #4: A child’s learning should be directed toward the “long view”
Here are ways we work to live out this assumption:
*The content and the experience of the content lead children to discover the deep principles of the domain and to develop inquiry strategies of wide applicability.
*Learning experiences target the enhancement of cognitive processes and learning mindsets.
*Critical thinking should be embedded in the basic concepts underlying the discipline.














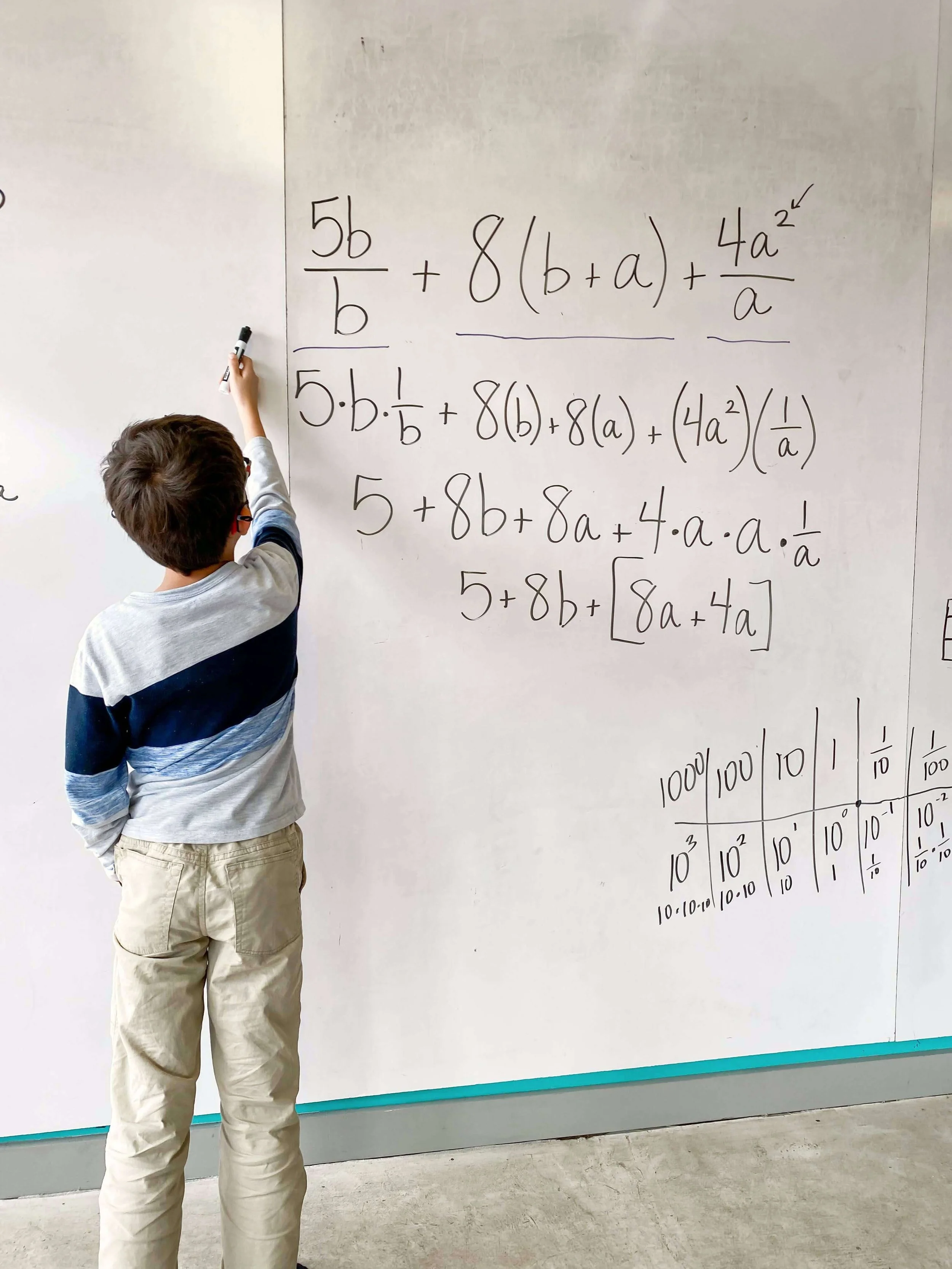






There is a hidden assumption about all numbers. Watch this video first.
There is a hidden assumption about number—we are always counting something. In this video, we help you transform your understanding of the concept of number. This should be the first video you watch.
In the video Different Forms, Still Counting, you can see how fractions and decimals can also be understood as counts. From there, you might be curious how we think about conducting a count, something like 17(5) which we read as "17 of 5" or " 17 fives." Either way, it is count of fives, and we have 17 of them. You may want to watch the video of Eric investigating ways to conduct that count of 17(5).